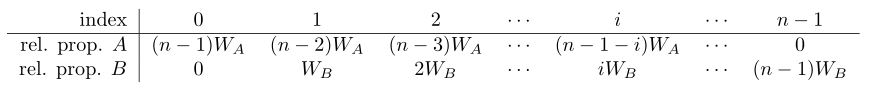This is about how to calculate the recipes for each of the glazes in a line blend. See here for the practicalities of making a line blend.
Suppose we have two glazes, A and B, and we want to make a line blend between them consisting of a certain number of glazes, which we’ll call n. How do we calculate the percentage of a material in a given glaze in the line blend?
To keep things simple, we’ll first assume that the batches of A and B have the same weight. We’ll label the glazes in the line blend using the index i, where i = 0 corresponds to A, and i = n - 1 corresponds to B. The table below shows the relative proportions into which A and B are divided.
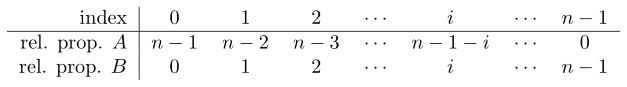
So the i-th glaze consists of n - 1 - i parts A and i parts B. To convert this to a percentage, we need to divide by n - 1 - i + i = n - 1 and multiply by 100%. Therefore the i-th glaze consists of (n - 1 - i) / (n - 1) 100% A and i / (n - 1) 100% B, so if PA is the percent of a material in recipe A, and PB is the percent of the same material in recipe B, the percent of that material in the i-th glaze is
(n - 1 - i) / (n - 1) PA + i / (n - 1) PB = [(n - 1 - i) PA + i PB] / (n - 1)
Now suppose that the weights of two batches are not necessarily equal, and have relative weights WA and WB. The table of relative proportions now looks as follows:
Therefore the i-th glaze consists of (n - 1 - i)WA parts A and i WB parts B, and to convert this to a percentage, we need to divide by (n - 1 - i)WA + i WB and multiply by 100%