This is a formula for determining the quantity of dry materials in a given quantity of glaze slurry. It is named after the former director of the Sèvres Porcelain Factory, Alexandre Brongniart.
There are a number of equivalent ways of expressing Brongniart’s formula. If Swet, Mwet, and Vwet are the specific gravity, mass, and volume of the slurry, and Sdry, Mdry, and Vdry are the specific gravity, mass, and volume[1] of the dry glaze materials, then
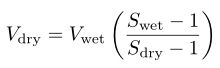. . . . . . . . . . . . . . . . . (1)
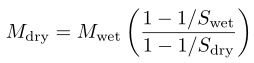. . . . . . . . . . . . . .(2)
Swet, Mwet, and Vwet can be measured, and for most glazes, Sdry is around 2.6 (exceptions are glazes which contain substantial amounts of tin or lead.). See the entry on the specific gravity of dry materials for a list of values.
If one substitutes Sdry = 2.6 into (2), the equation can be rewritten as
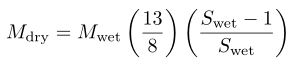
For example, 2kg of a glaze slurry with specific gravity 1.5 contains
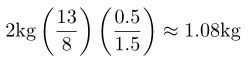
of dry materials.
Online calculator
https://pietermostert.github.io/SG_calc/html/brongniart.html
This requires the weight of the glaze slurry in the bucket, the weight of a syringeful of glaze slurry, and the weight of a syringeful of water (the ratio of the last two measurements gives the specific gravity of the glaze slurry). In theory, the weight of a syringeful of water in grams should equal volume of the syringe in millilitres, but syringes may be inaccurate. The default for the specific gravity of the dry materials is 2.6, but this can be changed.
-
Note that this is the volume of the water displaced by the dry materials. The volume of the dry materials will be larger since there are voids between the particles. ↩︎
